Have you ever looked at a math problem with mixed numbers and felt a little lost? Perhaps you’re trying to figure out how many batches of cookies you can make if each batch needs a certain amount of flour, and that flour is described using a whole number and a fraction. Or maybe you just want to understand the numbers better. Learning how to multiply mixed numbers can seem like a puzzle at first glance, but it's a skill that opens up a whole new level of confidence with numbers. It really does make a difference in how you approach math problems, giving you a clearer path forward.
Knowing how to multiply mixed numbers helps in many daily situations, not just in school. Think about cooking, building something, or even figuring out how much material you need for a project. These are all places where mixed numbers show up, and knowing how to work with them, especially multiplying them, makes those tasks much simpler. It's about being prepared for anything, as a matter of fact, just like you might prepare for other things in life.
Today, we're going to walk through the process of multiplying mixed numbers, step by step, making it easy to follow. We'll break down the concepts, provide clear examples, and give you the tools to handle these calculations with ease. You'll soon see that it's not as complicated as it might seem, so stick with us.
Table of Contents
- What Are Mixed Numbers, Anyway?
- Why Learn to Multiply Mixed Numbers?
- The Core Idea Behind Multiplication
- Getting Ready: Converting Mixed Numbers
- The Steps to Multiply Mixed Numbers
- A Practical Example to Walk Through
- Common Things to Watch Out For
- Frequently Asked Questions About Mixed Number Multiplication
- Bringing It All Together: Your Path to Mastery
What Are Mixed Numbers, Anyway?
A mixed number is simply a combination of a whole number and a fraction. For example, if you have two whole pizzas and one-half of another pizza, you have 2 1/2 pizzas. That's a mixed number. It shows a quantity that is more than a whole but not quite another full whole. You see these often in everyday life, so it's good to get a feel for them.
They are different from improper fractions, which have a top number (numerator) that is larger than or equal to the bottom number (denominator), like 5/2. Both mixed numbers and improper fractions represent the same kind of value, just in different forms. Knowing how to switch between them is a really helpful thing, you know, for when you're working with numbers.
Why Learn to Multiply Mixed Numbers?
Learning how to multiply mixed numbers helps you solve real-world problems that involve portions and groups. Imagine you are making a recipe that calls for 1 1/2 cups of sugar, and you want to make three times that amount. Without knowing how to multiply mixed numbers, figuring out the total sugar needed could be a bit of a challenge. This skill helps you get precise answers quickly.
It also builds a stronger foundation for more advanced math concepts later on. Being able to work with different forms of numbers, like these, shows a good grasp of how numbers behave. It’s a way of being prepared, which, as my text points out, is something that matters quite a bit in various aspects of life, including facing challenges and understanding what you need to do.
Everyday Examples
Think about a building project where each piece of wood needs to be 3 1/4 feet long, and you need 5 such pieces. To find the total length of wood, you would multiply 3 1/4 by 5. Or, consider a sewing project where each fabric panel uses 2 2/3 yards of cloth, and you plan to make 4 panels. You'd multiply to find the total yardage. These are just a few instances where this math comes into play, so it's a practical skill to have.
The Core Idea Behind Multiplication
Before we get into mixed numbers specifically, let's remember what multiplication is all about. My text explains that "the meaning of multiply is to increase in number especially greatly or in multiples." It also says that "multiplication is simply repeated addition." For example, 4 × 3 means adding 3 four times (3 + 3 + 3 + 3), which gives you 12. It's about combining groups of equal size.
You can also think of multiplication as scaling, where one number scales another. If you have 2 and you multiply it by 3, you are scaling 2 up by a factor of 3, resulting in 6. This basic idea remains true even when you work with mixed numbers. We're just applying this fundamental concept to a slightly different kind of number, so it's the same basic operation, just with a new format.
Getting Ready: Converting Mixed Numbers
The first and most important step when you want to multiply mixed numbers is to change them into improper fractions. This makes the multiplication process much simpler because you'll just be working with two fractions. Trying to multiply them in their mixed number form can be a bit messy and often leads to mistakes, so this conversion is really a key step.
It's like getting your ingredients ready before you start cooking. You wouldn't try to bake a cake with whole eggs in their shells, would you? You break them first. Similarly, you convert mixed numbers to improper fractions to make them easier to handle in the multiplication process. This preparation helps you avoid unnecessary steps or confusion, which, you know, can happen if you jump right in.
Step-by-Step Conversion
Let's say you have the mixed number 2 1/3. Here's how you turn it into an improper fraction:
- Multiply the whole number by the denominator: Take the whole number part (2) and multiply it by the bottom number of the fraction (3). So, 2 × 3 = 6. This step essentially tells you how many "thirds" are in the whole number part.
- Add the numerator to that product: Take the result from the last step (6) and add the top number of the fraction (1). So, 6 + 1 = 7. This gives you the total number of "thirds" you have.
- Place the new number over the original denominator: The new top number is 7, and the bottom number stays the same (3). So, 2 1/3 becomes 7/3. That's how you do it, pretty straightforward, in a way.
Let's try another one, say 3 2/5. You would do 3 × 5 = 15. Then, 15 + 2 = 17. So, 3 2/5 becomes 17/5. This process is quite consistent, and once you practice it a few times, it becomes second nature. You'll be able to do it almost without thinking, that's the goal.
The Steps to Multiply Mixed Numbers
Once you have both your mixed numbers converted into improper fractions, the rest is just like multiplying any other fractions. It's a series of clear actions, so you just follow them one by one. This method helps keep things organized and reduces the chances of making a mistake, which is always a good thing.
Step 1: Change to Improper Fractions
As we just talked about, this is your starting point. Take each mixed number in your problem and convert it into an improper fraction. For instance, if your problem is 2 1/3 × 3 2/5, you would convert 2 1/3 to 7/3 and 3 2/5 to 17/5. This step is absolutely essential for smooth sailing through the rest of the calculation. It really is the foundation for everything that follows.
Step 2: Multiply the Tops and Bottoms
Now that you have two improper fractions, you multiply their numerators (the top numbers) together, and you multiply their denominators (the bottom numbers) together. The product of the numerators becomes the new numerator, and the product of the denominators becomes the new denominator. For our example, (7/3) × (17/5):
- Multiply the numerators: 7 × 17 = 119
- Multiply the denominators: 3 × 5 = 15
So, the result of the multiplication is 119/15. This part is pretty simple, actually, just two straightforward multiplication problems.
Step 3: Simplify Your Answer
After you multiply, you might end up with a fraction that can be made simpler. This means finding a number that divides evenly into both the numerator and the denominator. If you can, divide both by that number to reduce the fraction to its simplest form. This makes the answer cleaner and easier to work with, in case you need to use it in another calculation.
For 119/15, we need to check if there are any common factors. 15 can be divided by 3 and 5. 119 is not divisible by 3 (1+1+9=11, not divisible by 3) and not by 5 (it doesn't end in 0 or 5). So, in this particular case, 119/15 is already in its simplest form. Sometimes, you might find a common factor, but sometimes you won't, so it's always good to check.
Step 4: Convert Back (If You Want To)
Your answer, 119/15, is an improper fraction. While mathematically correct, it's often helpful to convert it back to a mixed number, especially for real-world applications where a mixed number might make more sense. To do this, you divide the numerator by the denominator. The whole number part of the result is your new whole number, and the remainder becomes the new numerator, placed over the original denominator.
For 119/15:
- Divide 119 by 15.
- 15 goes into 119 seven times (15 × 7 = 105).
- The remainder is 119 - 105 = 14.
So, 119/15 as a mixed number is 7 14/15. This step is usually done to make the answer more intuitive, particularly if you are trying to explain it to someone or use it in a practical setting. It's like presenting your findings in a way that is easy for everyone to grasp, you know, for general clarity.
A Practical Example to Walk Through
Let's try a full example together: Multiply 1 1/4 by 2 1/2.
Step 1: Change to Improper Fractions
- For 1 1/4: (1 × 4) + 1 = 5. So, 1 1/4 becomes 5/4.
- For 2 1/2: (2 × 2) + 1 = 5. So, 2 1/2 becomes 5/2.
Now your problem looks like: (5/4) × (5/2). This is a really good start, as it sets everything up for the next stage.
Step 2: Multiply the Tops and Bottoms
- Multiply the numerators: 5 × 5 = 25.
- Multiply the denominators: 4 × 2 = 8.
Your new fraction is 25/8. This step, you know, is pretty straightforward once you have your improper fractions ready.
Step 3: Simplify Your Answer
Can 25/8 be simplified? 8 can be divided by 2, 4, and 8. 25 is not divisible by 2, 4, or 8. So, 25/8 is already in its simplest form. It's always a good habit to check, just in case there's a common factor hiding there.
Step 4: Convert Back (If You Want To)
To convert 25/8 back to a mixed number:
- Divide 25 by 8.
- 8 goes into 25 three times (8 × 3 = 24).
- The remainder is 25 - 24 = 1.
So, the final answer is 3 1/8. This complete process shows you how to handle a problem from start to finish. It really is a clear path to getting your answer.
Common Things to Watch Out For
When you're working through these problems, there are a few things that might trip you up if you're not paying attention. Staying alert to these common pitfalls can save you from making mistakes. It's a bit like being watchful for dangers, as my text suggests for other areas of life, so you can avoid falling into a trap.
- Forgetting to convert to improper fractions: This is the most frequent mistake. If you try to multiply mixed numbers directly, you'll likely get the wrong answer. Always convert first. It really makes the rest of the steps much easier.
- Errors in converting: Double-check your multiplication and addition when converting a mixed number to an improper fraction. A small error here will throw off your entire calculation. So, you know, take your time with this part.
- Not simplifying: While not always a mistake that makes the answer wrong, an unsimplified fraction is not considered the best form for a final answer. Always look for common factors. This makes your answer much cleaner, actually.
- Mistakes in multiplication of the numerators/denominators: Basic multiplication errors can happen, especially with larger numbers. A quick re-check of your multiplication facts can help. This is where precision matters, just a little bit more.
Frequently Asked Questions About Mixed Number Multiplication
People often have similar questions when they're learning how to multiply mixed numbers. Let's look at some of those, as a matter of fact, to help clear things up.
How do you multiply a mixed number by a whole number?
When you need to multiply a mixed number by a whole number, you follow the same steps. First, convert the mixed number into an improper fraction. Then, turn the whole number into a fraction by placing it over 1 (for example, 5 becomes 5/1). After that, you multiply the two fractions just like you learned: multiply the numerators together and the denominators together. Finally, simplify your answer and convert it back to a mixed number if you wish. It's really the same process, just with one of the numbers looking a bit different at the start.
Can you multiply mixed numbers without converting to improper fractions?
Technically, there are other ways to multiply mixed numbers, like using the distributive property, but they are often more involved and prone to errors. For instance, you could multiply the whole parts, then the whole part by the fraction, and so on, but this requires several separate calculations and then adding them all up. Most math educators and textbooks suggest converting to improper fractions because it streamlines the process significantly. It simplifies things quite a bit, so that's usually the recommended path. For more on fraction operations, you can learn more about fractions and decimals on our site.
What is the easiest way to multiply mixed numbers?
The method we've discussed—converting mixed numbers to improper fractions, multiplying the numerators and denominators, and then simplifying—is generally considered the simplest and most reliable way to multiply mixed numbers. It breaks down a seemingly complex problem into a series of straightforward steps that are easy to follow and apply consistently. This approach reduces confusion and helps you arrive at the correct answer efficiently. It's a pretty effective strategy, you know, for getting the job done right. You can find more helpful math resources by checking out this external math learning site, or link to this page for other math tips.
Bringing It All Together: Your Path to Mastery
Learning how to multiply mixed numbers is a very useful skill that helps you handle numbers with more confidence. We've gone through the steps: changing mixed numbers to improper fractions, multiplying the tops and bottoms, simplifying your result, and then turning it back into a mixed number if that makes sense for your situation. It's a clear process, and with a bit of practice, you'll find it becomes second nature. Just like learning any new skill, repetition helps you get better and faster.
Keep practicing these steps with different numbers. You can even make up your own problems to solve. The more you work with mixed numbers, the more comfortable you'll feel. This approach helps you build a solid understanding, which, in a way, is what learning is all about. So, keep at it, and you'll be multiplying mixed numbers like a pro in no time!


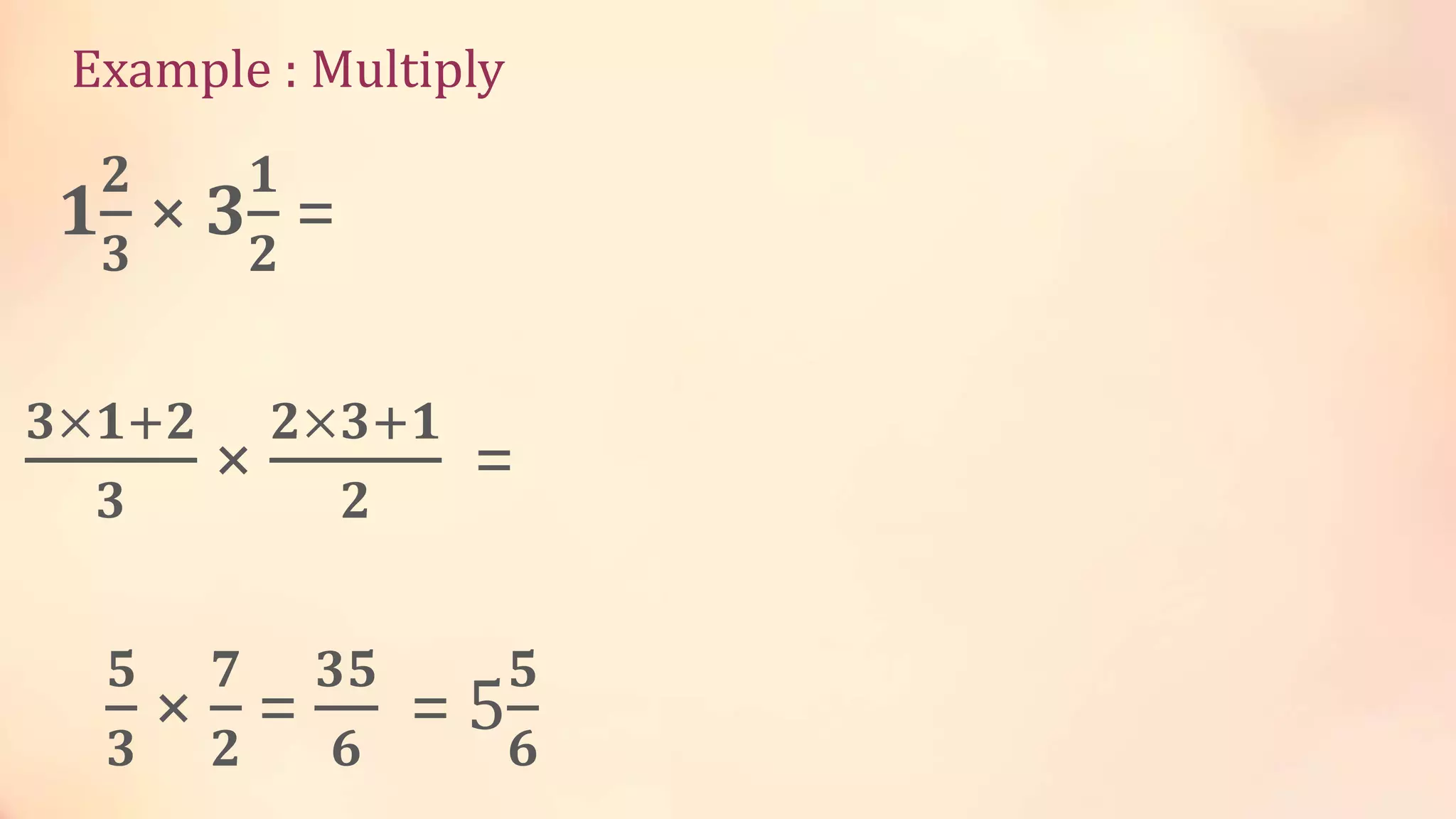
Detail Author:
- Name : Enola Marquardt
- Username : mozell84
- Email : weber.aliza@hotmail.com
- Birthdate : 1988-08-08
- Address : 21475 Donnelly Garden Jonathonmouth, IL 95842-3425
- Phone : +1-234-397-5538
- Company : Toy-Schuster
- Job : Floor Layer
- Bio : Suscipit delectus voluptas commodi praesentium. Mollitia occaecati dolorem nam nesciunt qui voluptas. Exercitationem ut qui aspernatur. Sunt ex corrupti iste qui facere itaque ut quia.
Socials
instagram:
- url : https://instagram.com/frunolfsson
- username : frunolfsson
- bio : Non recusandae eveniet et deleniti. Atque animi tenetur quo ut. Voluptate ex minus et quis ea.
- followers : 6420
- following : 194
facebook:
- url : https://facebook.com/fred792
- username : fred792
- bio : Id eaque placeat porro omnis deleniti dolor animi.
- followers : 690
- following : 1199

