Have you ever looked at a decimal, like 0.75, and wondered how it connects to a fraction, perhaps three-quarters? It's a pretty common question, and understanding how to convert decimals to fractions is a skill that truly helps in many everyday situations. Whether you're figuring out a recipe, working on a project around the house, or just trying to get a better handle on math, this ability is quite useful. So, as a matter of fact, let's explore how these two ways of showing parts of a whole are really just different faces of the same idea.

Think about it this way: numbers are like different languages we use to describe amounts. Decimals give us a smooth, continuous look at quantities, often seen with money or measurements. Fractions, on the other hand, show us specific parts of a whole thing, like slices of a pie. Both have their place, yet, knowing how to switch between them gives you more flexibility and a deeper grasp of what numbers truly mean. You know, it's pretty neat how they relate.

Just like our online tools help you quickly change measurement units, say, how many milliliters are in an ounce, or how many kilograms are in a newton, getting a grip on number conversions makes other calculations simpler, too. This guide aims to make the process of changing decimals into fractions as straightforward as possible, giving you the practical steps you need. It's really about building a good foundation for your number sense, you see.

• No Bake Oreo Cheesecake

Table of Contents

• Understanding Decimals and Fractions
• Why Learn This Conversion?
• The Simple Steps to Convert
  • Step 1: Figure Out the Place Value
  • Step 2: Write It as a Fraction Over a Power of Ten
  • Step 3: Make It Simpler
• Examples in Action
  • Example 1: A Basic Decimal (0.5)
  • Example 2: A Two-Digit Decimal (0.25)
  • Example 3: A Three-Digit Decimal (0.125)
  • Example 4: A Decimal with a Whole Number (2.75)
• Frequently Asked Questions About Decimal to Fraction Conversion
• Putting It All Together

Understanding Decimals and Fractions

Before we get into changing numbers, it helps to know what decimals and fractions actually are. A decimal, you know, is a way to show numbers that are not whole, using a point to separate the whole part from the part that is less than one. Each digit after the decimal point has a place value that is a power of ten, like tenths, hundredths, thousandths, and so on. It's really a system built on tens.

A fraction, by contrast, shows a part of a whole or a collection of equal parts. It has two main numbers: the top number, which is the numerator, and the bottom number, which is the denominator. The numerator tells you how many parts you have, and the denominator shows how many equal parts make up the whole thing. So, for instance, if you have a pizza cut into 8 slices and you eat 3, you've eaten 3/8 of the pizza. It's pretty straightforward, actually.

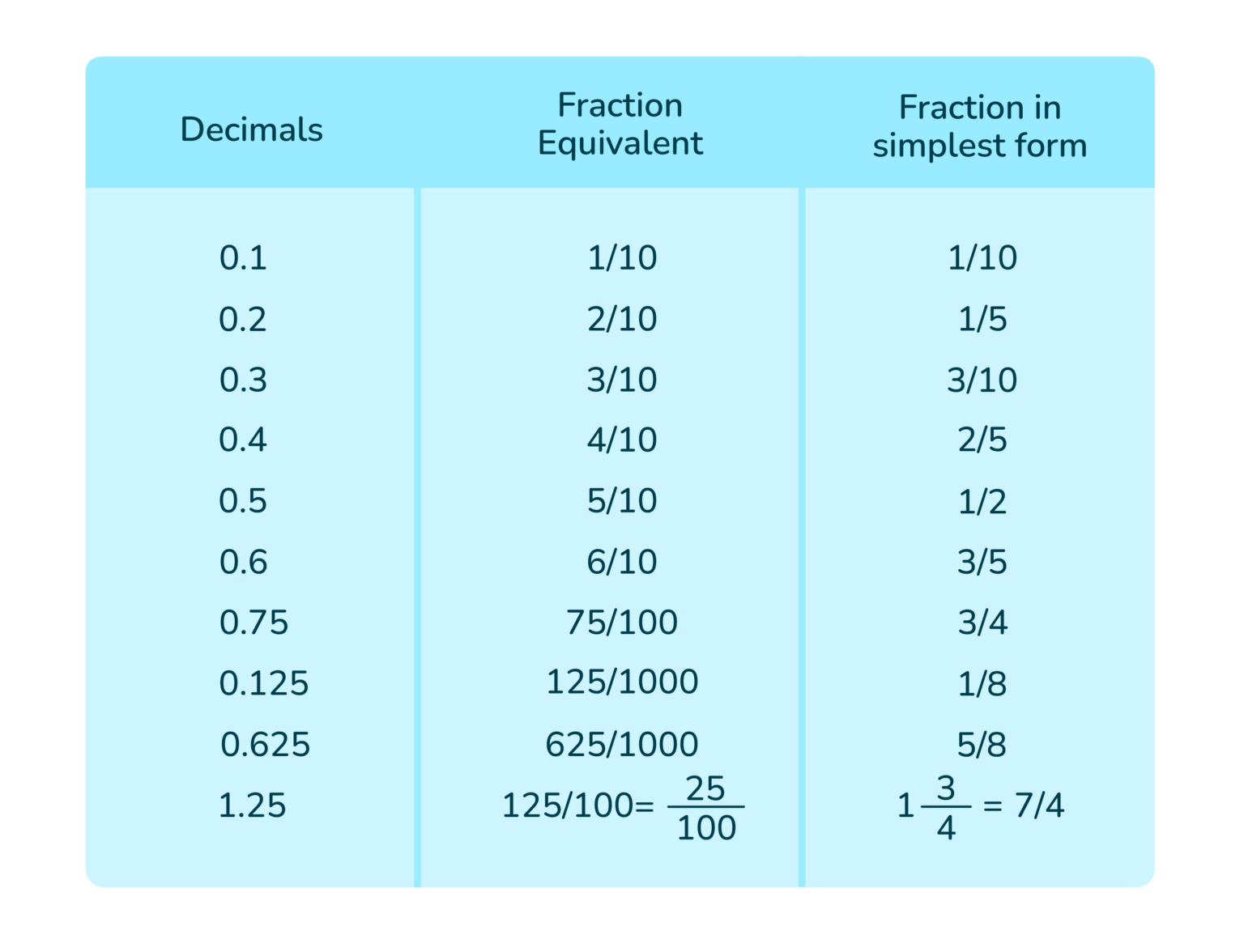
Both decimals and fractions are just different ways to express the same value, you see. For example, 0.5 and 1/2 represent the exact same amount. The trick is simply learning the steps to move from one form to the other. This skill is quite foundational for many math concepts, and it's something you'll use more often than you might think, too.

• I Guess Well Never Know

Why Learn This Conversion?

You might be wondering why it's worth your time to learn how to convert decimals to fractions. Well, for one thing, it often makes calculations easier. Sometimes, working with fractions can be much simpler than dealing with long decimals, especially when you're multiplying or dividing. So, it's a practical skill for doing math more efficiently, you know.

Beyond schoolwork, this conversion comes in handy in many real-world settings. Imagine you're baking and a recipe calls for "0.75 cups" of flour, but your measuring cups are marked in fractions. Knowing that 0.75 is the same as 3/4 makes it simple to measure correctly. Or, perhaps, you're doing a DIY project and need to cut a piece of wood to "0.875 inches." Converting that to 7/8 of an inch can make your measuring tape easier to read. It's quite useful, really.

Also, understanding how to convert between these forms strengthens your overall number sense. It helps you see the relationships between different types of numbers and builds a more complete picture of how they work. This deeper understanding can make future math topics, even things like algebra, feel a bit less intimidating. It's a foundational step, basically.

The Simple Steps to Convert

Converting a decimal to a fraction is a process that involves just a few clear steps. It's not nearly as complicated as it might seem at first glance. We'll break it down so you can follow along easily, you know. Just take it one step at a time, and you'll get the hang of it pretty quickly.

Step 1: Figure Out the Place Value

The very first thing you need to do is look at the decimal and find the last digit on the right. That digit's position tells you its place value. This place value will become the denominator of your initial fraction. For example, if the last digit is in the tenths place, your denominator will be 10. If it's in the hundredths place, it will be 100, and so on. It's quite simple, really, just count the places after the decimal point.

Let's say you have the decimal 0.7. The 7 is in the first spot after the decimal point, which is the tenths place. So, your denominator will be 10. If you have 0.25, the 5 is in the second spot after the decimal point, which is the hundredths place. Therefore, your denominator will be 100. This step is pretty important because it sets up the rest of your conversion, you see.

Remember, each place after the decimal represents a power of 10. One place means 10, two places mean 100, three places mean 1000, and so forth. This pattern is consistent, making it quite predictable. So, just count those spots, and you've got your starting point for the bottom number of your fraction, you know.

Step 2: Write It as a Fraction Over a Power of Ten

Once you've determined the place value from Step 1, you can write your decimal as a fraction. The number after the decimal point (without the decimal point itself) becomes your numerator. The place value you found in Step 1 becomes your denominator. So, for example, if you have 0.7, the number after the decimal is 7, and its place value is tenths (10). This means you write it as 7/10. It's really just putting the pieces together, you know.

Consider 0.25. The number after the decimal point is 25. The place value of the last digit (5) is the hundredths place, so the denominator is 100. This gives you the fraction 25/100. This step is pretty direct, basically, taking the decimal digits and putting them over the correct power of ten. It's like unwrapping the decimal to see its fractional form, you could say.

If your decimal has a whole number part, like 2.75, you can handle the whole number separately or convert the entire thing to an improper fraction. For 2.75, you'd treat the 0.75 as 75/100 first, and then add the whole number 2 back in as a mixed number (2 and 75/100). Or, you can think of 2.75 as 275 hundredths, making it 275/100 directly. Both ways work, you know, it just depends on what feels more comfortable for you.

Step 3: Make It Simpler

The final step, and often the most important, is to simplify the fraction you just created. Simplifying a fraction means finding the largest number that divides evenly into both the numerator and the denominator. This number is called the Greatest Common Factor, or GCF. You divide both the top and bottom numbers by this GCF until they can't be divided any further by a common number (other than 1). This makes the fraction as simple as it can be, you know, its most basic form.

Let's take our earlier example, 25/100. To simplify this, you look for numbers that divide both 25 and 100. You might notice that both numbers end in 5 or 0, so they are definitely divisible by 5. If you divide 25 by 5, you get 5. If you divide 100 by 5, you get 20. So now you have 5/20. You can still simplify this, can't you? Both 5 and 20 are divisible by 5 again. Divide 5 by 5 to get 1, and divide 20 by 5 to get 4. So, 25/100 simplifies to 1/4. It's quite a process of reduction, you see.

Sometimes, finding the GCF can be a bit tricky. A good strategy is to try dividing by small prime numbers like 2, 3, 5, 7, and so on. Keep dividing until you can't anymore. For instance, if you had 6/12, you could divide both by 2 to get 3/6, then divide both by 3 to get 1/2. Or, you might just see that 6 is the GCF right away and divide both by 6 to get 1/2. The goal is always the simplest form, basically, where the top and bottom numbers share no common factors other than one. This step truly makes the fraction easy to understand and use.

Examples in Action

Let's put these steps into practice with a few examples. Seeing how it works with different numbers can make the whole process much clearer, you know. We'll start with some pretty common decimals and work our way through them. It's a good way to get a feel for the method, really.

Example 1: A Basic Decimal (0.5)

Consider the decimal 0.5. This is a very common one, and it's a good starting point.

**Step 1: Figure Out the Place Value**
The digit 5 is in the first place after the decimal point. This means it's in the tenths place. So, our denominator will be 10. It's pretty direct, you see.

**Step 2: Write It as a Fraction Over a Power of Ten**
The number after the decimal point is 5. We place this over our denominator, 10. So, we get the fraction 5/10. This step is pretty straightforward, basically.

**Step 3: Make It Simpler**
Now we need to simplify 5/10. Both 5 and 10 can be divided by 5.
Divide the numerator (5) by 5: 5 ÷ 5 = 1.
Divide the denominator (10) by 5: 10 ÷ 5 = 2.
So, 0.5 converts to 1/2. It's a pretty neat way to see how they connect, you know.

Example 2: A Two-Digit Decimal (0.25)

Now let's try 0.25. This decimal has two digits after the point.

**Step 1: Figure Out the Place Value**
The last digit, 5, is in the second place after the decimal point. This means it's in the hundredths place. So, our denominator will be 100. This is a bit different from the last example, you know, but the rule stays the same.

**Step 2: Write It as a Fraction Over a Power of Ten**
The number after the decimal point is 25. We place this over our denominator, 100. This gives us the fraction 25/100. It's really just following the pattern, you see.

**Step 3: Make It Simpler**
We need to simplify 25/100. We can see that both numbers are divisible by 5.
Divide the numerator (25) by 5: 25 ÷ 5 = 5.
Divide the denominator (100) by 5: 100 ÷ 5 = 20.
Now we have 5/20. We can simplify this again, as both 5 and 20 are divisible by 5.
Divide the numerator (5) by 5: 5 ÷ 5 = 1.
Divide the denominator (20) by 5: 20 ÷ 5 = 4.
So, 0.25 converts to 1/4. It's pretty satisfying to get to that simplest form, you know.

Example 3: A Three-Digit Decimal (0.125)

Let's tackle 0.125. This one has three digits after the decimal point.

**Step 1: Figure Out the Place Value**
The last digit, 5, is in the third place after the decimal point. This means it's in the thousandths place. So, our denominator will be 1000. It's pretty consistent, isn't it?

**Step 2: Write It as a Fraction Over a Power of Ten**
The number after the decimal point is 125. We place this over our denominator, 1000. This gives us the fraction 125/1000. This part is really just writing it down, you know.

**Step 3: Make It Simpler**
Now we simplify 125/1000. Both numbers end in 5 or 0, so they are divisible by 5.
Divide the numerator (125) by 5: 125 ÷ 5 = 25.
Divide the denominator (1000) by 5: 1000 ÷ 5 = 200.
Now we have 25/200. Both are still divisible by 5.
Divide the numerator (25) by 5: 25 ÷ 5 = 5.
Divide the denominator (200) by 5: 200 ÷ 5 = 40.
Now we have 5/40. Still divisible by 5.
Divide the numerator (5) by 5: 5 ÷ 5 = 1.
Divide the denominator (40) by 5: 40 ÷ 5 = 8.
So, 0.125 converts to 1/8. This one took a few more steps to simplify, you know, but the process is the same. You can learn more about fractions on our site, for instance.

Example 4: A Decimal with a Whole Number (2.75)

What if the decimal has a whole number part, like 2.75?

**Option A: Convert the decimal part first, then add the whole number.**
Focus on the 0.75 part.
**Step 1:** The 5 is in the hundredths place, so the denominator is 100.
**Step 2:** Write as 75/100.
**Step 3:** Simplify 75/100. Both are divisible by 25 (or by 5 repeatedly).
75 ÷ 25 = 3.
100 ÷ 25 = 4.
So, 0.75 becomes 3/4.
Now, add the whole number back: 2 and 3/4. This is a mixed number. It's pretty straightforward, you know, to handle it this way.

**Option B: Convert the entire number to an improper fraction.**
Think of 2.75 as "two hundred seventy-five hundredths."
**Step 1:** The last digit, 5, is in the hundredths place. So the denominator is 100.
**Step 2:** Write the entire number without the decimal point as the numerator: 275. Place it over 100: 275/100. It's basically treating the whole number as part of the decimal, you see.

**Step 3: Make It Simpler**
Simplify 275/100. Both are divisible by 25.
275 ÷ 25 = 11.
100 ÷ 25 = 4.
So, 2.75 converts to 11/4. This is an improper fraction, which means the numerator is larger than the denominator. You can convert this to a mixed number by dividing 11 by 4 (11 ÷ 4 = 2 with a remainder of 3), which gives you 2 and 3/4. Both options lead to the same answer, you know, just by slightly different routes. It's really about choosing what feels most natural to you. Our site, which helps with conversions like how many cm^2 in 1 m^2, also helps with these foundational math ideas, too.

Frequently Asked Questions About Decimal to Fraction Conversion

People often have similar questions when they are learning how to convert decimals to fractions. Here are a few common ones, with some clear answers to help you out. It's pretty common to wonder about these things, you know.

How do you convert a decimal to a fraction step by step?

The process is quite simple, actually, and involves three main steps. First, you figure out the place value of the last digit in the decimal. This place value (like tenths, hundredths, thousandths) becomes the denominator of your initial fraction. Second, you write the digits after the decimal point as the numerator, placing them over that denominator. Third, and finally, you simplify the fraction by dividing both the numerator and the denominator by their greatest common factor until it can't be reduced any further. It's a very systematic approach, you see, making it easy to follow.

How do you convert a repeating decimal to a fraction?

Converting repeating decimals to fractions is a bit more involved than with terminating decimals, but it's still doable. For a simple repeating decimal like 0.333..., you can think of it as one-third. For more complex ones, a common method involves setting the decimal equal to a variable (say, x), then multiplying by a power of 10 to shift the repeating part. Subtracting the original equation from the new one helps cancel out the repeating part, leaving you with an equation you can solve for x, which will be your fraction. This method, while effective, is a bit beyond the basic steps for simple decimals. It's a slightly different kind of conversion, you know.

What is the easiest way to convert a decimal to a fraction?

The easiest way for most common decimals is to simply follow the three steps we outlined. Identify the place value of the last digit, write the decimal digits as the numerator over that place value (as a power of 10), and then simplify the resulting fraction. For example, 0.75 is 75 over 100, which simplifies to 3/4. This method is pretty quick for decimals that stop. Knowing your common fractions, like 0.5 is 1/2, or 0.25 is 1/4, also makes it faster because you might just recognize them. It's really about practice and getting familiar with the common ones, you know.

Putting It All Together

Learning how to convert decimals to fractions is a truly valuable skill that strengthens your overall number sense. By following the simple steps of identifying place value, writing the initial fraction, and then simplifying, you can confidently change any terminating decimal into its fractional form. This ability not only helps with homework but also proves useful in many everyday situations, from cooking to crafting. It's a foundational piece of math that just keeps giving, you know.

Keep in mind that practice makes perfect. The more you work through examples, the more natural and quicker these conversions will become. Don't be afraid to try different numbers and see how they break down. It's a skill that builds confidence, and soon you'll be seeing the connections between decimals and fractions with ease. You can explore more math concepts and conversion tools by checking out this external resource, for example. And for other helpful tools, you can always visit our main page for more information.